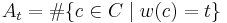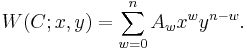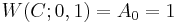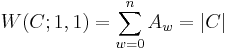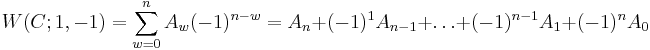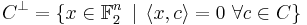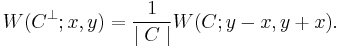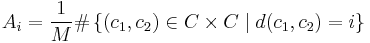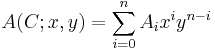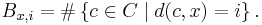Enumerator polynomial

In coding theory, the weight enumerator polynomial of a binary linear code specifies the number of words of each possible Hamming weight.

Let 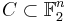C \subset \mathbb{F}_2^n be a binary linear code length n. The weight distribution is the sequence of numbers

A_t = \#\{c \in C \mid w(c) = t \}

giving the number of codewords c in C having weight t as t ranges from 0 to n. The weight enumerator is the bivariate polynomial

W(C;x,y) = \sum_{w=0}^n A_w x^w y^{n-w}.

Contents

Basic properties

  1. W(C;0,1) = A_{0}=1
  2. W(C;1,1) = \sum_{w=0}^{n}A_{w}=|C|
  3. W(C;1,0) = A_{n}= 1 \mbox{ iff } (1,\ldots,1)\in C\ \mbox{ and } 0 \mbox{ otherwise.}
  4. W(C;1,-1) = \sum_{w=0}^{n}A_{w}(-1)^{n-w} = A_{n}%2B(-1)^{1}A_{n-1}%2B\ldots%2B(-1)^{n-1}A_{1}%2B(-1)^{n}A_{0}

MacWilliams identity

Denote the dual code of 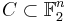C \subset \mathbb{F}_2^n by

C^\perp = \{x \in \mathbb{F}_2^n \,\mid\, \langle x,c\rangle = 0 \mbox{ }\forall c \in C \}

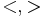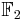(where <,> denotes the vector dot product and which is taken over \mathbb{F}_2).

The MacWilliams identity states that

W(C^\perp;x,y) = \frac{1}{\mid C \mid} W(C;y-x,y%2Bx).

The identity is named after Jessie MacWilliams.

Distance enumerator

The distance distribution or inner distribution of a code C of size M and length n is the sequence of numbers

A_i = \frac{1}{M} \# \left\lbrace (c_1,c_2) \in C \times C \mid d(c_1,c_2) = i \right\rbrace

where i ranges from 0 to n. The distance enumerator polynomial is

A(C;x,y) = \sum_{i=0}^n A_i x^i y^{n-i}

and when C is linear this is equal to the weight enumerator.

The outer distribution of C is the 2n-by-n+1 matrix B with rows indexed by elements of GF(2)n and columns indexed by integers 0...n, and entries

B_{x,i} = \# \left\lbrace c \in C \mid d(c,x) = i \right\rbrace .

The sum of the rows of B is M times the inner distribution vector (A0,...,An).

A code C is regular if the rows of B corresponding to the codewords of C are all equal.

References